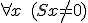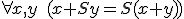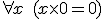Gödel : indémontrable mais vrai ?
Le 8 décembre 2007 par Sephi, dans Mathématiques
22 623 Visites | Version imprimable 
 Sommaire de l'article
Sommaire de l'article
- Énoncés des théorèmes d'incomplétude de Gödel
- Définitions préliminaires
- Première lecture des théorèmes d'incomplétude
- Seconde lecture des théorèmes : les conséquences
- 1. L'arithmétique de Peano PA et la théorie des ensembles ZF sont-elles consistantes ?
- 2. Existe-t-il une preuve absolue (i.e. non relative) de la consistance de PA et de ZF ?
- 3. Parmi les formules indécidables d'une théorie « convenable », y en a-t-il certaines qui sont vraies ?
- 4. La phrase de Gödel est-elle une formule méta-mathématique, ou une formule mathématique ?
- 5. Y a-t-il des propriétés mathématiques vraies et indémontrables ?
- 6. L'esprit humain surpasse-t-il toute machine ?
Définitions préliminaires
Une formule close est une formule logiquement valide sans variables libres (i.e. toute variable est quantifiée).
Exemple. La formule
est logiquement valide mais non close, exprimant que si x possède la propriété P, alors la relation R est vraie entre x et y. Par contre, la formule
est une formule close.
Une théorie est un ensemble (fini ou infini) de formules closes écrites avec des symboles puisés dans un ensemble de symboles appelé langage. Les éléments d’une théorie sont appelés axiomes. Voici des exemples importants :
Exemple. L’arithmétique élémentaire est la théorie écrite dans le langage
formée des sept axiomes suivants :
Ces axiomes permettent de formaliser l’ensemble des nombres naturels. La fonction S est le « successeur » qui, en pratique, associe à un naturel x le naturel x+1.
Exemple. L’arithmétique de Peano, que l’on notera PA, est obtenue à partir de l’arithmétique élémentaire en ajoutant l’axiome de récurrence1 qui affirme que pour vérifier qu’une propriété F est vraie pour tous les naturels, il suffit de montrer qu’elle est vraie pour 0, et que si elle est vraie pour un naturel x, alors elle est vraie pour son successeur Sx.
Exemple. La théorie des ensembles de Zermelo-Fraenkel (notée ZF) est l’ensemble formé des axiomes d’extensionnalité, de la paire, de la réunion, des parties, de l’infini et du schéma de remplacement. Le lecteur intéressé trouvera sans mal les définitions de ces axiomes. On retiendra que ZF permet de formaliser la totalité des mathématiques actuelles.
Une théorie est consistante si et seulement si elle est non-contradictoire, i.e. s’il est impossible de démontrer à la fois une formule et sa négation.
Une théorie est récursive s’il est possible de déterminer (en un nombre fini d’étapes) si une formule F donnée fait partie des axiomes de la théorie.
Exemple. Toute théorie formée d’un nombre infini d’axiomes est non récursive.
Une formule F est décidable dans une théorie T si cette dernière démontre F ou sa négation, i.e. si on peut déterminer à partir des axiomes de T, et avec les règles d’inférence de la logique classique, si F est vraie ou fausse.
Une théorie est complète si et seulement si elle est consistante et si toute formule F est décidable.
Nous avons maintenant en main tous les outils pour comprendre les énoncés des théorèmes de Gödel.
- En fait, ce n’est pas l’axiome de récurrence mais le schéma de récurrence qui est ajouté. Je me suis permis cet abus pour ne pas alourdir le texte. [↩]