---

Témoignages sur le phénomène de l’intuition

Bien qu’il soit discutable de parler de réelle connaissance à ce stade, l’histoire regorge de témoignages de mathématiciens racontant des expériences durant lesquelles un résultat ou une solution à un problème se sont imposés spontanément à l’esprit, sans raisonnement préalable.

Finalement, il y a deux jours, j’ai réussi… Comme en un éclair subit, l’énigme se trouva résolue. [Gauss]

Au moment où je mettais le pied sur le marchepied, l’idée me vint, sans que rien dans mes pensées antérieures parût m’y avoir préparé. [Poincaré]

Ayant été réveillé très brusquement par un bruit extérieur, une solution longuement cherchée m’apparut immédiatement, sans le moindre instant de réflexion de ma part. [Hadamard]

Le phénomène sous-jacent, qu’il est raisonnable de désigner par intuition, est celui qui nous intéressera dans ce texte. Remarquons d’abord trois caractéristiques sur lesquelles je m’attarderai par la suite, mises en évidence dans les trois citations :

Les deux dernières affirmations semblent se contredire, mais nous verrons que ce n’est pas le cas.

Première définition

Dans un premier temps, je propose de définir l’intuition en mathématiques comme étant une idée qui, dès son apparition, conquiert le coeur du mathématicien. Même si ce dernier ne peut pas encore affirmer que son intuition constitue un réel résultat (pour cela, il faudrait qu’il y ajoute un développement rigoureux), cela n’empêche qu’il a la forte conviction d’être sur le bon chemin.

L’idée intuitive n’étonne guère par son excentricité, mais plus souvent par son aspect d’évidence manquée par le conscient. Le mathématicien s’exclame « Mais c’est bien sûr ! » avant de se lancer dans un travail de vérification consistant à prouver que son intuition était la bonne.

Andreas Speiser¹ utilise l’exemple très évocateur suivant. Comment prouver le théorème disant que la somme des angles d’un triangle vaut 180° ? En cas d’hésitation, il suffit de proposer la piste suivante : tracer la parallèle à un des côtés, passant par le sommet opposé.

Le théorème se démontre alors immédiatement par des considérations sur les angles alternes internes. Speiser écrit à ce sujet :

Lorsque l’on a trouvé la bonne construction, tout s’éclaire d’une seule considération intellectuelle et l’on n’a plus besoin de clés formelles. Souvent la découverte de la bonne construction demande un travail de longues années et la réussite se manifeste parfois par une illumination brutale. Tous les grands mathématiciens et les artistes nous racontent de tels moments de bonheur.

L’illumination brutale dont parle Speiser n’est autre que ce que j’appelle intuition. Nous verrons que, loin d’être un phénomène aléatoire, l’intuition est un processus de l’esprit dont une étude célèbre nous a été faite, entre autres, par Henri Poincaré et Jacques Hadamard.

Mais avant de se pencher en détail sur le sujet, on peut d’abord se poser deux questions à propos de l’intuition : s’agit-il d’un phénomène conscient ? Est-il aléatoire ?

Si on se réfère aux précédentes citations, il est clair que l’intuition ne fait pas partie du conscient, ce qui est exprimé par le fait qu’elle apparaisse sous la forme d’une étonnante illumination soudaine. Hadamard a eu son intuition à un moment où il ne pensait absolument pas aux mathématiques : lors d’un brusque réveil ! L’intuition n’est pas non plus un phénomène aléatoire : elle apparaît souvent pour apporter une solution à un problème qui préoccupait déjà le mathématicien, même s’il n’y travaillait pas au moment précis où se produit l’illumination.

On penchera vers l’hypothèse que l’intuition est un processus inconscient, ce que Poincaré exprime :

Ce qui vous frappera tout d’abord, ce sont ces apparences d’illumination subite, signes manifestes d’un long travail inconscient.

L’intuition en quatre étapes

C’est pendant que vous essayez de comprendre et que vous ne trouvez pas, que vous faites le trou. [Alain Connes]

Cette curieuse phrase qu’Alain Connes a prononcée lors d’un entretien pour la chaîne Arte décrit en fait le premier stade dans le processus qui mène à une intuition.

Tout d’abord, le mathématicien est confronté à une question qu’il va essayer de résoudre consciemment. Supposons que la question soit extrêmement ardue, à un point tel que malgré tous ses efforts et ses approches différentes, le mathématicien ne voit aucune piste sur laquelle se lancer.

À ce stade, à défaut de cerner la solution, on pourrait dire que le mathématicien a acquis, non sans mal, une bonne compréhension du problème. C’est l’étape qu’Hadamard appelle la préparation, durant laquelle le mathématicien se fidélise au problème. En général, il faut au moins quelques jours d’efforts intenses et infructueux pour que l’on puisse parler de préparation. (Le « trou » dont parle Alain Connes, c’est celui que l’on creuse dans le mur des obstacles, pour atteindre la solution qui se trouve derrière.)

La seconde étape vient naturellement lorsque le mathématicien déclare forfait et abandonne provisoirement le problème. Il tourne alors son esprit vers d’autres occupations et intérêts. Cependant, son inconscient va prendre le relais et continuer ses investigations sur la question. Libéré ainsi de la pression qui pesait sur le conscient, l’inconscient peut travailler dans une plus grande liberté et explorer un plus grand éventail de pistes. Suivant Hadamard, c’est l’étape de l’incubation.

On pourrait prendre comme métaphore celle d’un archéologue qui cherche un hiéroglyphe précis sur un énorme mur couvert de symboles. Imaginons qu’il soit dans le noir et doive s’aider d’une lampe de poche dont il peut régler la taille du faisceau. Le travail conscient correspondrait à chercher le hiéroglyphe avec un faisceau intense, mais très concentré de sorte qu’il ne couvre qu’une petite zone du mur à la fois. Un tel travail est précis mais très lent.

Lors de l’incubation, le travail de l’inconscient correspondrait à utiliser un faisceau plus diffus (qui, dans l’obscurité, rendrait les symboles moins distincts), mais qui couvre une plus grande zone. Il est alors possible d’apercevoir plus rapidement, moyennant une certaine imprécision, le hiéroglyphe recherché.

Si cela se produit, l’inconscient communique sa trouvaille au conscient par le biais d’une illumination subite : c’est la troisième étape. Il suffit alors de reprendre sa lampe avec un faisceau que l’on concentre cette fois sur la nouvelle piste. C’est l’étape de la vérification consciente de la piste obtenue par intuition.

Résumons brièvement les quatres étapes qui interviennent dans le processus de l’intuition :

Cependant, une question demeure : que fait exactement l’inconscient durant l’incubation ?

L’inconscient et la beauté mathématique

En général, quand on étudie un problème donné, on essaie de combiner ensemble divers éléments déjà connus (typiquement des propriétés, des théorèmes, des exemples…) dans l’espoir de trouver, par associations d’idées, la bonne solution.

D’après Hadamard, le travail de l’inconscient consiste justement à réaliser des combinaisons d’idées, mais d’une façon plus libre que ne le fait le conscient. Si ce dernier ne cherche que du côté des idées liées au problème traité, l’inconscient peut travailler avec des idées provenant d’ailleurs, sans lien direct avec le sujet.

Ainsi, l’inconscient explore un éventail de possibilités plus large. Une illumination se produit lorsqu’il tombe sur une combinaison « remarquable » et la communique au conscient. L’apparition d’une intuition, c’est donc finalement le résultat d’une sélection : celle des combinaisons « remarquables » d’idées. Inventer, c’est choisir (Hadamard).

Mais quel est le critère suivant lequel l’inconscient juge du caractère remarquable d’une combinaison d’idées ? Il semblerait que ce critère ne soit rien d’autre que l’élégance, la beauté mathématique de la combinaison en question.

La question complexe de l’esthétique en mathématiques mériterait un ouvrage entier, et je serais bien incapable de la traiter. Je me contenterai ici de mentionner subjectivement quelques aspects qui interviennent dans un résultat mathématique perçu comme élégant.

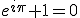
Ainsi, l’intuition serait un processus inconscient qui accompagne le travail conscient en effectuant librement des combinaisons d’idées et en sélectionnant celles qui satisfont à des critères d’élégance mathématique. Je ne résiste pas au plaisir de citer une très belle phrase d’Alain Connes à ce sujet, que l’on pourrait même prendre comme une seconde définition :

L’intuition, c’est la tension vers la beauté.

L’intuition comme moteur

Bien que la plupart des citations et exemples qui précèdent sont tirés de grands mathématiciens, il est bon de remarquer que l’intuition est un processus qui intervient chez tout mathématicien impliqué dans une activité de recherche mentale. De plus, l’intuition n’est évidemment pas exclusive au mathématicien, loin de là ! En réalité, elle semble être présente dans toute activité de création mentale, notamment en poésie où elle est décrite d’une façon fort proche de l’activité mathématique comme le témoigne le poète Paul Valéry :

Ce qu’on appelle « génie » est bien moins l’acte qui combine, que la promptitude à comprendre la valeur de ce qui vient de se produire et à saisir ce produit.

L’intuition agit comme moteur car elle fournit une piste prometteuse au mathématicien qui, impatient, va s’empresser de la vérifier (ce qui peut représenter un travail laborieux). Cette vérification est nécessaire et importante, car une intuition peut bien sûr être erronée (le contraire eût été trop beau).

Prendre conscience du rôle de l’intuition apporte également une vision très optimiste de l’activité mathématique. La première étape nécessaire au processus intuitif est la préparation durant laquelle le mathématicien, qu’il soit apprenti ou expérimenté, reste désarmé face au problème malgré ses efforts. Loin d’être un échec, il s’agit en fait d’un stade nécessaire pour aller plus loin et atteindre, dans le meilleur des cas, la bonne solution. Sécher sur un problème, c’est avancer vers sa résolution.

Poincaré me semble être la meilleure personne pour apporter la conclusion à cet article :

C’est par la logique que nous prouvons, c’est par l’intuition que nous inventons.

 
 
 

Références :