Le génie de la numération babylonienne
Le 8 novembre 2006 par Sephi, dans Mathématiques
On sait généralement que la Mésopotamie a vu naître l’écriture. Ce qui est moins connu, c’est qu’elle est également le berceau d’une des premières grandes activités mathématiques du monde. Tout cela, c’est grâce à un système de numération particulièrement performant.
L’origine : la civilisation sumérienne
On attribue aux Sumériens l’invention de l’écriture vers l’an -3300 de notre ère. Ils sont également les auteurs du premier système de numération qui, malheureusement, n’était pas des plus pratiques.
En effet, seuls des nombres entiers positifs pouvaient être représentés. Le système était d’ailleurs plutôt laborieux. Six petits objets fabriqués avec de la terre, appelés calculi, désignaient les quantités 1, 10, 60, 600, 3600 et 36 000. On voit déjà l’ébauche d’une numération en base 60, malgré la présence du nombre 10.

Un nombre était représenté de manière très concrète : les calculi qui composaient ce nombre étaient placés dans une boule creuse en terre cuite, que l’on refermait et marquait d’un sceau. Pour connaître le nombre associé à cette boule, il fallait la briser et compter les calculi à l’intérieur.
Par la suite, on a commencé à graver sur les boules des empreintes indiquant leur contenu. Elles étaient faites à l’aide d’une tige de roseau de forme cylindrique : le calame. Les calculi devenaient donc inutiles et on a fini par les abandonner. Les boules d’argile ont été aplaties pour former des tablettes, sur lesquelles on gravait les nombres.

Ces tablettes servaient essentiellement à faire de la comptabilité. La tablette la plus complexe (découverte à Shuruppak et datant de -2650 environ) contient le simple problème de division suivant :
(I) On donne un grenier d’orge.
(II) 7 silà
(III) chaque homme reçoit.
(IV) Combien sont ces hommes ?
Un silà était une mesure de capacité (environ 0,842 litre) et un grenier d’orge valait 1 152 000 silà. La réponse est donnée dans la partie inférieure de la tablette :
(V) 164 571
(VI) Il reste 3 silà.
Le développement : la civilisation akkadienne
Vers -2500, les Akkadiens envahissent Sumer, absorbent puis développent la culture sumérienne. La civilisation akkadienne atteint son apogée vers -1700 avec le roi Hammurabi (célèbre pour le premier code de lois du monde). Sa capitale Babylone était aussi son centre intellectuel, avec plus d’1 million de tablettes retrouvées. Environ 300 d’entre elles sont de nature mathématique et seront étudiées par Otto Neugebauer et Thureau-Dangin à partir de 1935.
Un des apports fondamentaux des Akkadiens est la simplification de l’écriture pictographique sumérienne. Le calame cylindrique est remplacé par un calame à base triangulaire, ce qui permet de produire les deux symboles principaux de l’écriture akkadienne : le clou  et le chevron
et le chevron  . Ces deux symboles sont à la base de l’écriture cunéiforme (du latin cuneus : « le clou »). Cette écriture sera déchiffrée en 1857 par Sir Rawlinson, ce qui permettra de constater que les mathématiques babyloniennes étaient déjà avancées bien avant l’arrivée des grecs.
. Ces deux symboles sont à la base de l’écriture cunéiforme (du latin cuneus : « le clou »). Cette écriture sera déchiffrée en 1857 par Sir Rawlinson, ce qui permettra de constater que les mathématiques babyloniennes étaient déjà avancées bien avant l’arrivée des grecs.
Le système de numération babylonien
Il s’agit d’une numération de position en base mixte 10 et 60. Un clou  vaut 1 et est répété au plus 9 fois. Un chevron
vaut 1 et est répété au plus 9 fois. Un chevron  vaut 10 et est répété au plus 5 fois. C’est seulement à partir du nombre 60 que le principe de position s’applique.
vaut 10 et est répété au plus 5 fois. C’est seulement à partir du nombre 60 que le principe de position s’applique.
Quelques exemples de nombres :

 = 35
= 35
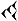
 = 1×60+42 = 102
= 1×60+42 = 102
Neugebauer utilise la notation 1,42.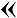

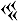
 = 21×60+58 = 1318
= 21×60+58 = 1318
Alternativement : 21,58.
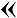

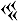

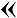
 = 1×603+28×602+52×60+21 = 319 941
= 1×603+28×602+52×60+21 = 319 941
Alternativement : 1,28,52,21.
Un fait troublant est l’absence du symbole zéro ! Pour représenter un nombre comme 3601 = 1×602+0×60+1, il fallait insérer un espace vide :  __
__  , où __ représente l’espace. Avec plusieurs zéros consécutifs, la notation deviendrait problématique. Heureusement, les Séleucides introduiront un symbole pour le zéro vers -300 environ.
, où __ représente l’espace. Avec plusieurs zéros consécutifs, la notation deviendrait problématique. Heureusement, les Séleucides introduiront un symbole pour le zéro vers -300 environ.
Un autre fait troublant est l’absence de virgule, ce qui fait que les nombres sont notés en « virgule flottante » ! Un nombre tel que 

 peut donc désigner 11×602+10×60, ou 11×60+10, ou encore 11+10×60-1. La conséquence directe est que les fractions se notent de la même façon que les nombres entiers … Pour savoir quel nombre était désigné, il fallait donc se référer au contexte.
peut donc désigner 11×602+10×60, ou 11×60+10, ou encore 11+10×60-1. La conséquence directe est que les fractions se notent de la même façon que les nombres entiers … Pour savoir quel nombre était désigné, il fallait donc se référer au contexte.
Un exemple de fraction est donné par 
 , qui peut représenter le nombre 7×60-1+30×60-2 = 1/8. Neugebauer utilise la notation suivante : 0;7,30.
, qui peut représenter le nombre 7×60-1+30×60-2 = 1/8. Neugebauer utilise la notation suivante : 0;7,30.
On peut remarquer que le nombre 1/7, par exemple, possède un développement sexagésimal illimité : 0;8,34,17,88,34,17 … Cependant, les babyloniens n’avaient pas l’équivalent des points de suspension. Il semble qu’ils évitaient tout simplement de représenter de tels nombres.
De manière générale, un nombre 1/n (où n est un entier) possède un développement sexagésimal limité si et seulement si n = 2A3B5C, où A, B et C sont des entiers. Dans ce cas, on dit que n est un entier régulier. Dans notre système décimal, n est régulier si et seulement si n = 2A5B.
En particulier, tous les multiples de 3 admettent une représentation finie dans le système babylonien, ce qui n’est pas le cas avec notre système décimal actuel. Le système babylonien est donc plus pratique que le nôtre ! Le génie de la numération babylonienne a permis à cette civilisation antique de développer des mathématiques beaucoup plus complexes que ce que l’on pense. Parmi les résultats qui figurent sur les tablettes retrouvées, on peut citer :
- Une approximation de
 , correcte jusqu’à la cinquième décimale ! (Tablette YBC 7289)
, correcte jusqu’à la cinquième décimale ! (Tablette YBC 7289) - La première approximation de pi de l’Histoire. (Tablette de Suse)
- Une résolution d’équations du second degré. (Tablette BM 13901)
- Une utilisation de la formule (non démontrée) de Pythagore, avant la naissance de celui-ci ! (Tablettes BM 85196 et Plimpton 322)
- La résolution de certaines équations non-linéaires à 2 (voire 3 !) inconnues.
- Une certaine connaissance des rapports de longueurs dans des triangles rectangles semblages.
Cliquez ici pour imprimer.

