Principia » Imprimer » Pi et racine de 2 chez les babyloniens

Pi et racine de 2 chez les babyloniens

Le 19 février 2007 par Sephi, dans Mathématiques

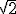Pour illustrer la grande richesse des mathématiques babyloniennes, bien en avance sur leur temps, nous étudions ici deux tablettes cunéiformes où apparaissent deux célébrités numériques : $\pi$ et $\sqrt2$ .

(Pour savoir comment lire le système de numération babylonien utilisé ici, se référer à l’article Le génie de la numération babylonienne.)

Une première approximation de pi

La première approximation connue du nombre $\pi$ provient des Babyloniens. Considérons la reproduction suivante d’une tablette de Suse :

Il s’agit en fait d’une table donnant l’aire (colonne de gauche) d’une série de figures (colonne de droite). Un premier exemple est donné à la ligne 27 :

2;37,30 IGIGUB SASAG 6

qui signifie :

2,625 est la constante du polygone régulier à 6 côtés

La « constante » désigne ici l’aire et correspond (approximativement) à celle d’un hexagone régulier dont les côtés sont de longueur 1.

Regardons maintenant la deuxième ligne :

0;5 IGIGUB SAGAM

qui signifie :

1/12 est la constante du cercle

Cette fois-ci, c’est le périmètre du cercle qui est supposé valoir 1. On en déduit donc la valeur du rayon :

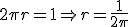
${2}\pi r = 1 \Rightarrow r = \frac1{2\pi}$

et l’aire vaut :

$\frac1{12} = \pi r^2 = \frac1{4\pi}$

On en tire que la valeur de $\pi$ est 3. C’est une approximation un peu grossière, bien qu’on la retrouve aussi chez les Chinois et dans la Bible.

On peut cependant jeter un oeil à la ligne 30 :

0;57,36 IGIGUB SASAR

qui signifie :

24/25 = 0,96 est la constante du cercle amélioré

Pour comprendre ce qu’est un « cercle amélioré », multiplions cette valeur par l’aire du cercle donnée à la ligne 2 :

$\frac1{12} \times \frac{24}{25} = \frac2{25}$

Si on suppose que cette dernière valeur est l’aire d’un cercle, on peut en déduire la valeur de $\pi$ qui est :

$\pi = \frac{25}8 = 3,125$

Voilà une bien meilleure approximation ! On comprend alors que la quantité 0;57,36 = 24/25 est le facteur de correction à apporter à l’aire du cercle donnée à la ligne 2 pour obtenir une valeur plus précise, d’où l’expression « cercle amélioré ».

Cette approximation est assez remarquable pour l’époque, car il faudra attendre plus de 15 siècles et l’arrivée d’Archimède pour avoir une meilleure approximation.

Racine de 2

On attribue généralement les premières mentions du nombre 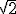$\sqrt2$ à l’école de Pythagore vers -500. Pourtant, cette fameuse diagonale du carré apparaît déjà chez les Babyloniens. Considérons la tablette YBC 7289, vraisemblablement utilisée par un écolier :

À quoi correspondent les nombres inscrits sur ce carré dont les diagonales ont été tracées ? Regardons-les d’un peu plus près.

Le premier nombre est qui vaut 30. Vu son emplacement, il désigne probablement la longueur du côté du carré.
Il y a deux nombres à l’intérieur du carré. Le premier, situé sur la diagonale horizontale, est . Sachant qu’une écriture babylonienne peut correspondre à plusieurs nombres, on peut se demander si celui-ci est un entier. Vu qu’il semble désigner la diagonale d’un carré de côté 30, on va tenter d’opter pour la réponse négative, et supposer qu’il s’écrit, en notation de Neugebauer, comme 1;24,51,10. En développant cette hypothèse, on a :

1 + 24/60 + 51/60² + 10/60³ ≈ 1,41421296

C’est une approximation de $\sqrt 2$ correcte jusqu’à la cinquième décimale !
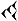
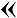
Pour confirmer leur connaissance de cette quantité particulière dans le carré, on peut maintenant regarder le deuxième nombre, situé en-dessous : que l’on supposera être 42;25,35. En développant, on a :

42 + 25/60 + 35/60² ≈ 42,426389

qui n’est autre qu’une approximation, avec 3 décimales correctes, de la longueur de la diagonale valant $30\sqrt 2$ .

Il est donc vraisemblable que les scribes babyloniens avaient connaissance du rôle de $\sqrt 2$ dans le lien entre le côté d’un carré et sa diagonale. Par contre, rien n’indique qu’ils avaient une idée du caractère irrationnel (ou incommensurable) de ce nombre. Cette tablette reste remarquable quand on pense qu’il faudra attendre encore plus de 12 siècles avant de voir réapparaître $\sqrt 2$ chez les Grecs.

Cliquez ici pour imprimer.