Principia

177 869 Visites | Version imprimable

Son idée de la démonstration

Le livre de Carr, peu représentatif des mathématiques « académiques » et au contenu parfois déséquilibré, a constitué la principale source d’enseignement pour Ramanujan en Inde, étant donné qu’il n’a pas pu intégrer l’université. Ses lacunes sont donc le reflet du contenu du livre. Par exemple, Hardy écrit :

Je doute fort que Ramanujan ait jamais clairement compris, et ce jusqu’à sa mort, en quoi consiste une fonction analytique.

De plus, sa méthode de travail s’est fortement inspirée de la présentation du livre. Ceci se traduit par une négligence quasi totale de la démonstration, ce qui est illustré par cette citation de Littlewood :

Il ne possédait peut-être pas du tout l’idée de ce qui est signifié par une démonstration, notion si familière aujourd’hui qu’elle est considérée comme acquise; si un bout signifiant de raisonnement lui venait quelque part à l’esprit, et que, globalement, le mélange entre intuition et évidence lui donnait quelque certitude, il n’allait pas plus loin.

Le travail de Ramanujan était donc essentiellement basé sur son intuition. Ce manque de rigueur constituera son principal handicap dans sa carrière, notamment lorsqu’il s’intéressera à la théorie analytique des nombres.

Selon Hardy, c’est dans ce domaine que Ramanujan a connu un échec réel :

Il fit preuve, comme toujours, d’une puissance d’imagination renversante, mais sa démonstration était quasiment inexistante, et même, une grande partie de ce qu’il avait imaginé se révéla faux.

Hardy fait surtout allusion au théorème des nombres premiers, selon lequel la quantité de nombres premiers compris entre 0 et x est approximé, lorsque 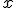est très grand, par , ce que l’on note :

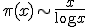
À l’époque de Hardy, la démonstration de ce théorème faisait un usage intensif des propriétés de la fonction de Riemann, définie pour toute variable complexe par :

Or, une des lacunes de Ramanujan était précisément l’analyse complexe. Hardy commente ce fait :

La théorie de Ramanujan sur les nombres premiers a été faussée du fait de son ignorance de la théorie des fonctions d’une variable complexe. … Que ses démonstrations n’aient pas été valables, c’était prévisible. Mais les erreurs étaient plus profondes, et la plupart des résultats présentés étaient faux. … Ceci fut un des grands échecs de Ramanujan.

Il convient de nuancer ce dernier passage. En effet, Hardy était de nature particulièrement sévère vis-à-vis des mathématiques. Il a même déclaré une fois que :

Cet échec était plus étonnant que n’importe lequel de ses [ceux de Ramanujan] triomphes.

ce qui est assez impitoyable, quand on pense que Ramanujan a découvert tout seul la forme du théorème des nombres premiers et que dans ce domaine, il compte parmi ses prédécesseurs des noms tels que Legendre, Dirichlet ou Gauss !

De plus, Hardy pensait fermement que l’analyse complexe et la théorie des fonctions analytiques étaient le cadre naturel d’étude de la distribution des nombres premiers, d’où l’importance considérable qu’il accordait à ces domaines. Cependant, ce théorème a été démontré par Paul Erdös et Atle Selberg en 1949 (deux ans après la mort de Hardy) avec « seulement » des outils élémentaires de l’analyse réelle.

L’avis de Hardy reste intéressant car il révèle un peu mieux la relation entre lui et le génie indien. D’ailleurs, Hardy était lui-même conscient de ses jugements parfois trop sévères. Nous pouvons terminer par cette dernière conclusion de Hardy, dans laquelle il rétablit l’admiration immense qu’il a toujours eue pour Ramanujan :

Nous pourrions affirmer beaucoup plus sûrement que son échec est tel qu’au total, il doit renforcer notre admiration envers ses dons et non la diminuer : il nous fournit en effet une preuve supplémentaire et surprenante de son imagination, de sa souplesse d’esprit.

 
 
 

Références :

Pages : « 1 2 3 4 5 6 7

---

Trackback URI |