L’intuition en mathématiques
Le 30 septembre 2007 par Sephi, dans Philo des sciences
37 650 Visites | Version imprimable 
 Sommaire de l'article
Sommaire de l'article
L’inconscient et la beauté mathématique
En général, quand on étudie un problème donné, on essaie de combiner ensemble divers éléments déjà connus (typiquement des propriétés, des théorèmes, des exemples…) dans l’espoir de trouver, par associations d’idées, la bonne solution.
D’après Hadamard, le travail de l’inconscient consiste justement à réaliser des combinaisons d’idées, mais d’une façon plus libre que ne le fait le conscient. Si ce dernier ne cherche que du côté des idées liées au problème traité, l’inconscient peut travailler avec des idées provenant d’ailleurs, sans lien direct avec le sujet.
Ainsi, l’inconscient explore un éventail de possibilités plus large. Une illumination se produit lorsqu’il tombe sur une combinaison « remarquable » et la communique au conscient. L’apparition d’une intuition, c’est donc finalement le résultat d’une sélection : celle des combinaisons « remarquables » d’idées. Inventer, c’est choisir (Hadamard).
Mais quel est le critère suivant lequel l’inconscient juge du caractère remarquable d’une combinaison d’idées ? Il semblerait que ce critère ne soit rien d’autre que l’élégance, la beauté mathématique de la combinaison en question.
La question complexe de l’esthétique en mathématiques mériterait un ouvrage entier, et je serais bien incapable de la traiter. Je me contenterai ici de mentionner subjectivement quelques aspects qui interviennent dans un résultat mathématique perçu comme élégant.
- La symétrie, et plus généralement la notion d’invariance. Ces considérations sont très fortes dans les mathématiques liées à la physique. Un objet (abstrait ou géométrique) qui est invariant sous certaines transformations traduit l’idée que cet objet renferme quelque chose de fondamental et d’essentiel. Des pans entiers des mathématiques se sont consacrés à l’étude de structures invariantes, comme la prolifique théorie des groupes.
- La généralité d’un résultat. Il est aisé de se dire qu’un théorème qui repose sur des hypothèses très faibles possède une généralité beaucoup plus grande que le simple exemple particulier. La généralité traduit ici une idée de « puissance » qui participe à l’élégance du théorème.
- Ce que j’appelle l’unité d’un résultat avec la théorie qui l’englobe. Certains résultats relient entre eux des entités mathématiques a priori très éloignés (au sens où ils sont définis dans des cadres totalement différents). Le fait que ces entités se retrouvent dans un même résultat est alors surprenant et suscite un étonnement admiratif. Un exemple connu est l’identité d’Euler, qu’un sondage réalisé en 2004 par le magazine Physics World a déclaré comme étant « la plus grande équation de tous les temps » :
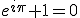
Ainsi, l’intuition serait un processus inconscient qui accompagne le travail conscient en effectuant librement des combinaisons d’idées et en sélectionnant celles qui satisfont à des critères d’élégance mathématique. Je ne résiste pas au plaisir de citer une très belle phrase d’Alain Connes à ce sujet, que l’on pourrait même prendre comme une seconde définition :
L’intuition, c’est la tension vers la beauté.


